1.前言
在微机保护装置中,首先要对反映被保护设备的电气量(电压、电流)进行采集,然后对这些采集的数据进行数字滤波,再对这些经过数字滤波的数字信号进行数学运算、逻辑运算,并进行分析判断,最终输出跳闸命令、信号命令或计算结果,以实现各种继电保护功能。目前,实现模拟量计算幅值的算法有很多,而傅立叶算法在微机保护中作为计算信号幅值的算法被广泛采用,不但可以求出各次谐波分量的幅值和相角,而且具有一定的滤波作用,可有效滤除恒定直流分量和各正次谐波分量。
2.傅里叶算法原理
那么,到底什么是傅里叶变换算法?傅里叶变换(Fourier transform)是一种线性的积分变换。因其基本思想首先由法国学者傅里叶系统提出,所以以其名字来命名以示纪念。
傅里叶变换一般分为连续傅里叶变换和离散傅里叶变换,电力系统中电气量(电压、电流)在进入微机保护装置后,软件通过AD对模拟量进行固定采样频率的等间隔采样,会得到一组周期性的离散信号,我们以此信号来计算出相应幅值和相角。因此,这里应用的是离散傅里叶变换,其变换公式如下:
傅氏算法的基本思路来自傅里叶级数,一个周期函数满足狄里赫利条件,就可以将这个周期函数分解为一个级数,即一个周期性函数可以分解为直流分量、基波分量及各次谐波的无穷级数,如下表示:
据傅氏级数的原理,可以求出 、 分别如下:
上述公式中 表示基波角频率; 和 分别是各次谐波的正弦和余弦的幅值,其中比较特殊的有: 表示直流分量, 表示基波分量正、余弦项的幅值。根据上述公式计算各次谐波时,是通过对余弦各值进行周期性的累加,所以就消除了直流分量 的影响。
已知获得的各次谐波的正弦和余弦的幅值 和 ,即可得到谐波有效的幅值及应用相角θn。

3.软件实现
软件通过AD对模拟量进行固定采样频率的等间隔采样,设每周波采样点为N,即w1=2π/N,采样次数为k。 和 可变换为:
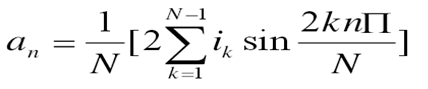
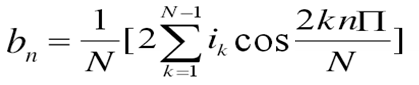
这里我们来计算信号的基波分量,首先求出基波分量(n=1)的实部和虚部 。以我公司最新继电保护装置为例,采用32位高性能SoC嵌入式微机处理器,大容量的RAM和Flash Memory,高精度AD,每周波采样点数N=128,则每周波采样值分别是i0、i1、i2……i127,同时其对应的基波正弦和余弦系数如下表所示。

基波正弦和余弦系数(N=128)
根据上述公式,进行基波正、余弦的系数累计相加,于是可得:

由此即可进一步计算出相应的幅值和相位。
基础软件开发部 羊阳
